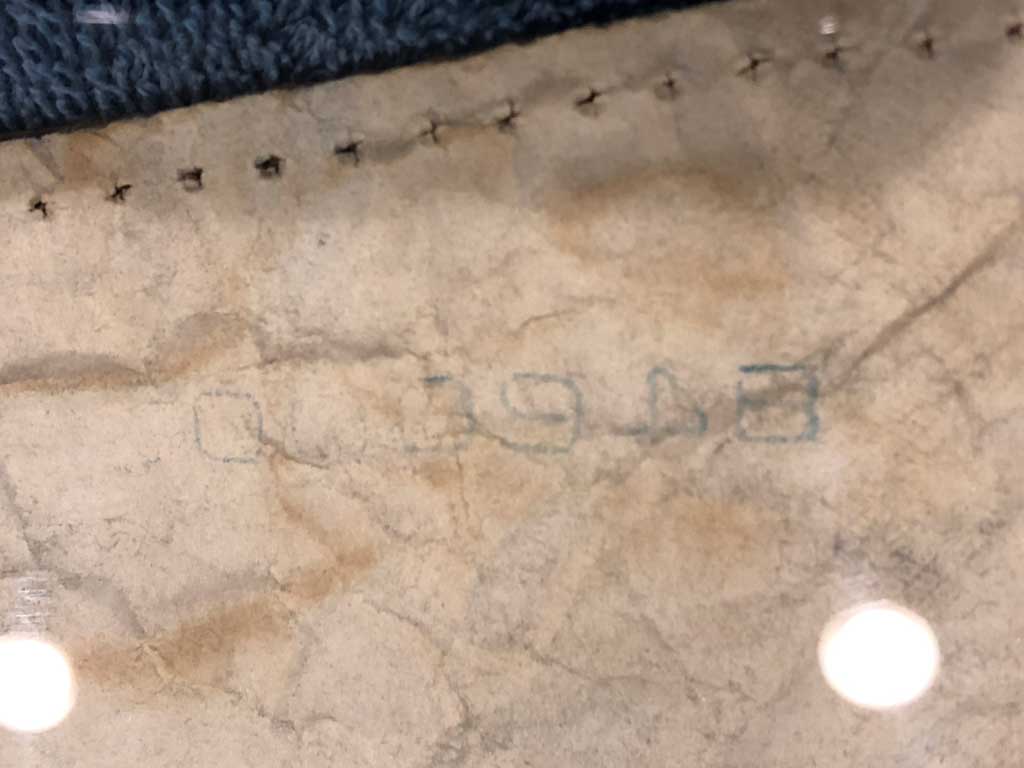Burn Test: 1984 Kingsford vs 2020 Kingsford

In This Topic

• Video: Burn Test – 1984 Kingsford vs 2020 Kingsford
• Where Did You Get A Bag Of 1984 Kingsford Charcoal?
• Product Packaging
• What Kingsford Says About 1984 Briquets
• What Kingsford Says About 2020 Briquets
• Comparing Performance Of New & Old Products
• Product Comparison Photos
• Weight Difference Before Burning
• The Burn Test
• Weight & Volume Difference Of Ashes After Burn Test
• Conclusions
• Estimating The Age Of This Old Bag Of Kingsford Charcoal
• More Kingsford Links On TVWB

Video: Burn Test – 1984 Kingsford vs 2020 Kingsford

This video summarizes the burn test results discussed in this article. It also includes a time-lapse of the first 13 minutes of the burn test.

Where Did You Get A Bag Of 1984 Kingsford Charcoal?

In April 2019, I was contacted by a member of The Virtual Weber Bulletin Board named Mike in Roseville. A friend of his acquired a vintage, barely used, mid- to late-1970s 22″ black Weber kettle with a flower-pattern cover, a new-in-box Weber side table, several unopened bags of off-brand charcoal, and this open, partially used bag of Kingsford. Having no need for the charcoal, the friend offered it to Mike. Knowing that I had done a series of Kingsford charcoal burn tests over the years, Mike offered up this charcoal to me for a burn test comparing it to today’s Kingsford.

I got the bag of charcoal from Mike on May 4, 2019. Due to my busy schedule, laziness, and procrastination, I didn’t get around to conducting the burn test until June 30, 2020. Upon examination, the bag contained about 4 pounds of charcoal, including lots of bits and pieces and charcoal dust. I was able to salvage 50 whole briquets for this burn test.

After doing some research, I arrived at 1984 as the most likely age of this charcoal. You can read about my investigation and ultimate decision on age at the end of this article.

Product Packaging

Here’s a photo of the 20-pound 1984 Kingsford bag next to an 8-pound 2020 Kingsford bag. You may recall that a man at the grill appeared on the front of Kingsford bags for many years.

What Kingsford Says About 1984 Briquets

Kingsford made the following claims on the 1984 bag:

• Lights fast and easy
• Easy Open – Pull Red Tear Strip From Right To Left
• Start your fire at least 1/2 hour before barbecuing
• 20 LBS NET WT
• A Product Of Kingsford Company • Oakland CA 94623
• © 1978 KFD CO.

What Kingsford Says About 2020 Briquets

Kingsford makes the following claims on the 2020 bag:

• Made with 100% natural ingredients
• The Way BBQ Should Taste
• The First. The Best. The Original.
• Since 1920
• 8 LB
• About 2 uses
• Made in the USA with North American ingredients

Since 2006, many of Kingsford’s product claims have focused on faster lighting charcoal. You’ll notice that the old bag said to allow “at least 1/2 hour” for lighting, while in recent years bags have shouted “Ready faster!” followed a few years later by “Ready EVEN faster!” I assume the race for faster lighting charcoal is to draw people away from the 10 minute pre-heat of their gas grills and back to their charcoal kettles.

It’s also interesting to note that the 2020 bag touts claims of natural ingredients, local sourcing of materials, authenticity, and tradition. These are the same attributes that many consumers are looking for today in the foods they buy.

Comparing Performance Of New & Old Products

While I did give some thought to actually grilling with this old bag of K, not knowing how old charcoal degrades over decades led me to the more prudent decision to conduct a burn test comparing the old and current Kingsford briquets.

The objective was to see:

• Which charcoal appeared to light the fastest
• Which charcoal appeared to burn the longest
• Which charcoal produced the least ash by weight and volume

Product Comparison Photos

Here are side-by-side photos of both briquets. The 1984 Kingsford briquet was slightly rectangular in shape, a bit longer but a bit narrower than the 2020 version which is essentially square. The 1984 K was also thicker than its 2020 counterpart.

The 2020 version features the trademark “K” stamped into one side and the two diagonal Sure Fire Grooves stamped into the other side, while the 1984 version has neither. We’ve lost track of when Kingsford added the “K” to its briquets, but the vertical Sure Fire Grooves were added in 2006 and turned diagonal in 2010.

Here’s a better view of the crackled surface of the 1984 briquets. In the second photo, there’s a small piece of unburned wood sticking out of a briquet. There were a few briquets in the bag that looked similar to this one.

Weight Difference Before Burning

I counted out 50 of each briquet and weighed them using an electronic kitchen scale.

The weight of each pan was noted in grams, then the net weight of
50 briquets, then the briquet name.

Here’s the net weigh of each batch of briquets:

50 Briquets (1984)	50 Briquets (2020)
1324 g / 2.92 lbs	1160 g / 2.56 lbs

 

2020 Kingsford briquets weigh less than 1984 briquets because they contain more lightweight wood char and less coal.

On average:

• A 1984 Kingsford Original briquet weighed 26.48 g / 0.934 oz.
• A 2020 Kingsford Original briquet weighted 23.20 g / 0.818 oz.

The Burn Test

I conducted this burn test on June 30, 2020.

I placed 50 of each briquet in identical Weber chimney starters and lit the charcoal with one Weber lighter cube. Unlike burning in the vent-controlled environment of a Weber smoker, this was an uncontrolled burn test—I just lit the charcoal and watched what happened over the next 80 minutes.

Each chimney starter was placed over a disposable foil pan so I could measure the weight and volume of ash produced after burning. Some ash was lost during the burn test—it got carried away by the heat rising out of the chimney starter (a light dusting of ash covered the area around the gas grill upon which I conducted the test)—but this test would still provide a good sense of which charcoal produces the most ash and which produces the least.

During the first 5 minutes of lighting, the 1984 briquets gave off more smoke and a whiter smoke than the 2020 briquets. Starting at around 6 minutes, 1984 Kingsford pretty much stopped smoking, while 2020 Kingsford kept giving off a reduced amount of smoke for another 3 minutes.

What follows are side-by-side photos comparing the burn of each product over 80 minutes.

It’s clear that today’s Kingsford lights faster than its 1984 counterpart. At 5 minutes, there is more fire deep in the 2020 briquets and at 10 minutes strong fire at the top of the charcoal and lots of gray ashing on the briquets. It appeared that 2020 K was ready for cooking at about the 7 minute mark, while 1984 K was ready at about the 10 minute mark.

Due to my smartphone overheating in the presence of these chimney starters, there were no photos captured between 10 minutes and 25 minutes. Once the phone cooled off, at 25 minutes there is very intense fire burning in the 1984 Kingsford while the 2020 version has calmed down significantly.

Notice that during the last 50 minutes, the 1984 Kingsford appears to burn longer and hotter than the 2020 Kingsford. At 45 minutes, I used a ThermoWorks infrared thermometer to measure the 1984 charcoal burning at about 700°F, the 2020 charcoal burning at about 500°F.

Weight & Volume Difference Of Ashes After Burn Test

After 80 minutes, I tapped each chimney so that all ashes fell into the foil pan below. I poured the leftover hot coals onto the grate and let them cool. What you see in this photo is the unburned charcoal that was too large to fall through the grate.

I placed the leftover charcoal in each foil pan and let it burn out completely and cool overnight. The next day I weighed each pan and subtracted the weight of the pan to determine the net weight of the ashes. To measure the volume of ashes, I used the “dip & sweep” method using measuring cups, similar to how you measure flour when baking.

	Kingsford Original 1984	Kingsford Original 2020
Net Weight of Ashes	273 g / 9.63 oz	255 g / 8.99 oz
Volume of Ashes	2-3/8 cups	3-5/8 cups
Percentage of Ashes	273 g ÷ 1324 g = 20.6%	255 g ÷ 1160 g = 22%

 

In the following two photos, you can see a marked difference in texture between 1984 Kingsford ashes which are coarse and sand-like versus 2020 Kingsford ashes which are fine and powder-like.

Conclusions

In an uncontrolled burn test:

• 2020 Kingsford Original Briquets lit faster than 1984 Kingsford Original Briquets. This makes sense because Kingsford made significant changes in briquet design and ingredients in 2006, 2010, and 2015 to make the product light faster.
• 1984 Kingsford appeared to burn slightly longer than 2020 Kingsford. My subjective evaluation of the photos leads me to believe the 2020 charcoal had a useful burn time of about 43 minutes (from about 7 min. to 50 min. timestamp) while the 1984 charcoal had a useful burn time of about 55 minutes (estimated to be from 10 min. to 65 min. timestamp). I suspect this is due to the formula containing more coal and each briquet weighing 14% more than a 2020 briquet.
• 1984 Kingsford and 2020 Kingsford produced about the same weight and the same percentage of ashes, but 2020 Kingsford produced 53% more ashes by volume than 1984 Kingsford.

It’s important to remember that this was a test of 36 year old charcoal, not new briquets made using the 1984 formula. I don’t know all the details about how charcoal briquets deteriorate over a long period of time. I do know that old charcoal can absorb moisture and become hard to light, but that did not seem to be the case with these briquets.

Estimating The Age Of This Old Bag Of Kingsford Charcoal

Today, Kingsford charcoal has production information printed on the back of the bag in the bottom right corner.

• The first two characters represent the manufacturing plant where the briquets were made.
• The next two numbers represent the last two digits of the year when the briquets were packed. In this example, “20” means the year 2020.
• The next three numbers represent the Julian calendar day when the briquets were packed. In this example, “003” means January 3.
• The final number represents the time in 24 hour format when the briquets were packed. In this example, “13:50” means 1:50 PM.

So these briquets were packed on January 3, 2020 at 1:50 PM.

Figuring out the age of the old Kingsford Briquets was not so easy.

Mike in Roseville, the fellow who gave me the charcoal, felt it dated to somewhere around the copyright date shown on the bag—1978-1980—based on the age of the kettle and accessories with which it was found.

You can see the copyright date shown on the front of the bag in the bottom right corner.

However, the copyright date on the bag has to do with the design of the bag, its graphics, text, and color scheme, not its contents.

A closer examination of the bag shows two production stamps near the top opening of the bag.

Both codes appear to be flipped horizontally. The first two digits are much clearer in the second instance, but it’s missing the last digit shown in the first instance.

When you flip over these images and combine them, you get what appears to be 84e0002.

This code does not match exactly the format used on current Kingsford bags, but I assume that 84 is the year, e0 is the manufacturing plant, and 002 is the Julian calendar day. If so, this bag was packed on January 2, 1984.

I sent these photos to TVWBB member and Kingsford retiree Mike Barger. He forwarded them to a contact at the Kingsford plant in Belle, Missouri. They could not provide a definitive answer, but their best guess was the late 1980s.

I also sent these photos to Kingsford customer support. They could not provide an authoritative answer on the code format, but they did agree that “84” for 1984 was a reasonable assumption.

1984. That’s my story and I’m sticking to it…until proven otherwise.

More Kingsford Links On TVWB

• Burn Test 2022: Kingsford Original vs Franklin Barbecue vs B&B Competition Oak Charcoal Briquets
• Kingsford Long-Burning Charcoal Briquets & Weber 100% All Natural Hardwood Charcoal Briquettes Burn Test 2017
• Kingsford Professional Briquets Replace Competition Briquets
• New Kingsford Original Charcoal Briquets Formula For 2015
• Kingsford Charcoal Briquets – Minor Changes For 2010
• Kingsford Competition Briquets – New For 2009
• Kingsford Charcoal Briquets – New Design, New Formula For 2006
• Kingsford R&D Lab Trip Report
• All About Charcoal

Back to Operating Tips & Modifications